S. Bachthaler,
F. Sadlo,
C. Dachsbacher,
D. Weiskopf:
In Proceedings of International Conference on Information Visualization Theory and Applications (IVAPP),
pp. 573–583,
2012.
|
|
Abstract
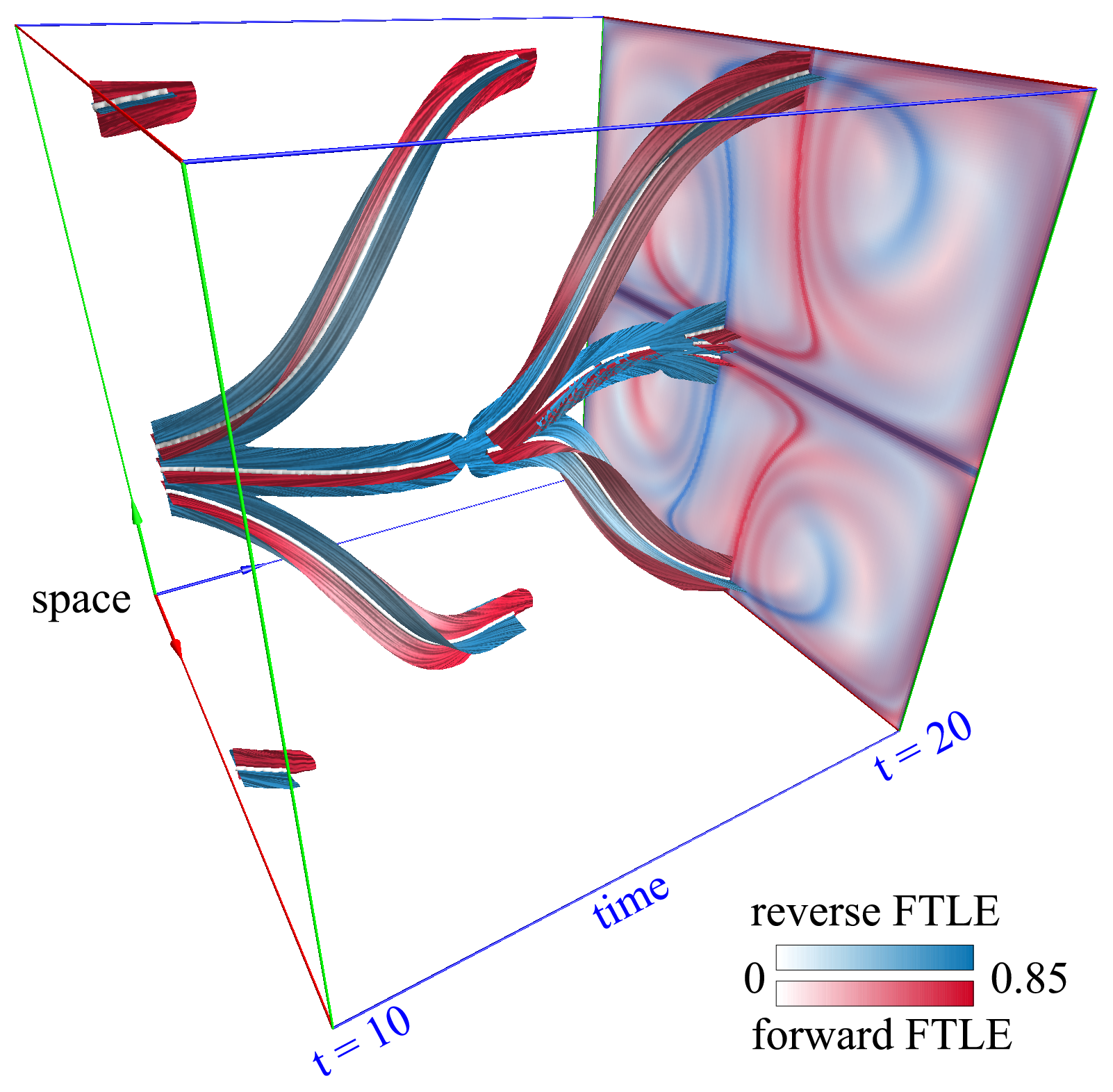
Lagrangian coherent structures (LCS), apparent as ridges in the finite-time Lyapunov exponent (FTLE) field, represent a time-dependent alternative to the concept of separatrices in vector field topology. Traditionally, LCS are analyzed and visualized in terms of their geometric shape only, neglecting stretching and compression in tangent directions. These effects are, however, of particular interest in mixing phenomena and turbulence. Hyperbolicity plays an important role in these processes and gives rise to hyperbolic trajectories originating at the intersections of forward and reverse LCS. Since integration of hyperbolic trajectories is difficult, we propose to visualize the corresponding space-time intersection curves of LCS instead. By stacking the traditional 2D FTLE video frames of time-dependent vector fields, a space-time FTLE field is obtained. In this field, ridge lines turn into ridge surfaces representing LCS, and their intersection forms curves that are a robust alternative
to hyperbolic trajectories. Additionally, we use a space-time representation of the time-dependent vector field, leading to a steady 3D space-time vector field. In this field, the LCS become stream surfaces given that their advection property is sufficiently met. This makes visualization of the dynamics within LCS amenable to line integral convolution (LIC), conveying in particular the dynamics around hyperbolic trajectories. To avoid occlusion, the LCS can be constrained to space-time bands around the intersection curves, resembling visualization by saddle connectors. We evaluate our approach using synthetic, simulated, and measured vector fields.
|
Available Files
[BibTeX]
[PDF]
|
|

