R. Peikert,
F. Sadlo:
In Topology-Based Methods in Visualization II, Springer Berlin Heidelberg,
pp. 145–160,
2009.
|
|
|
Abstract
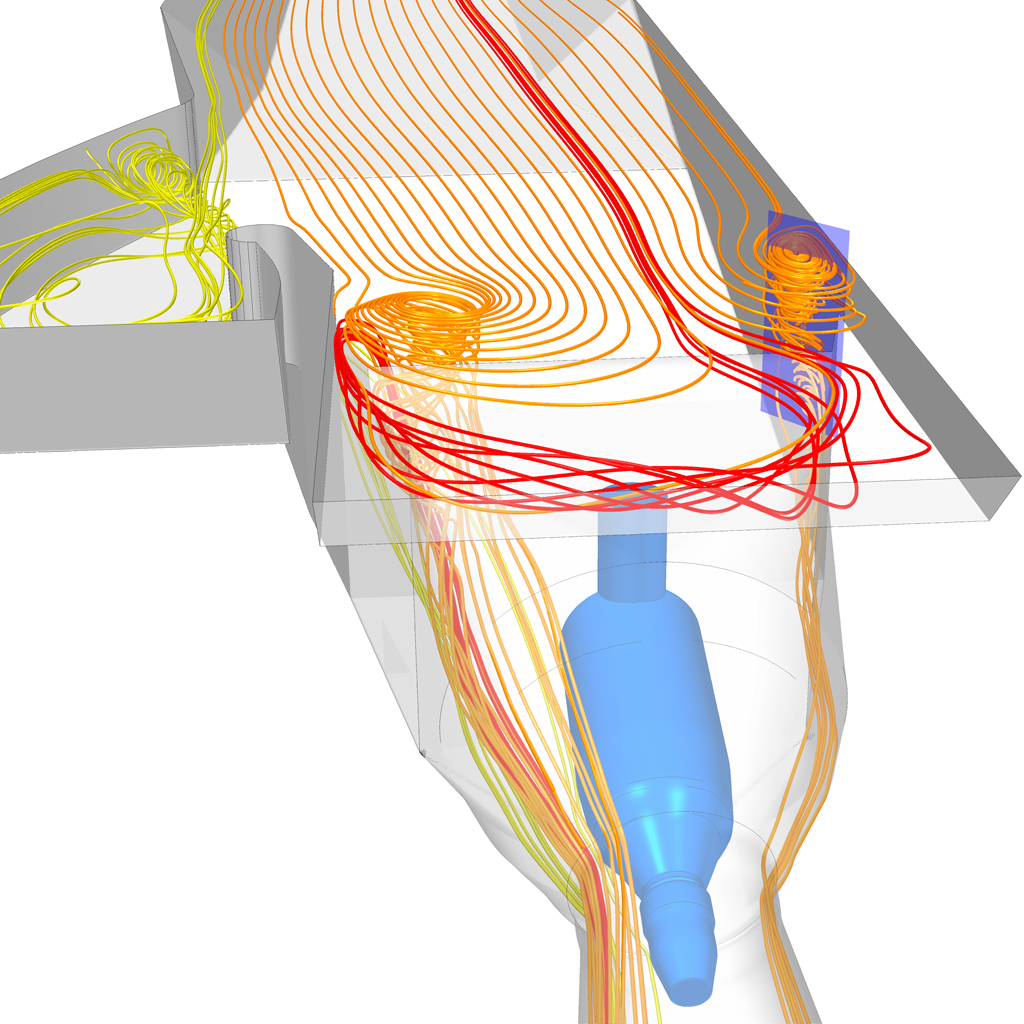
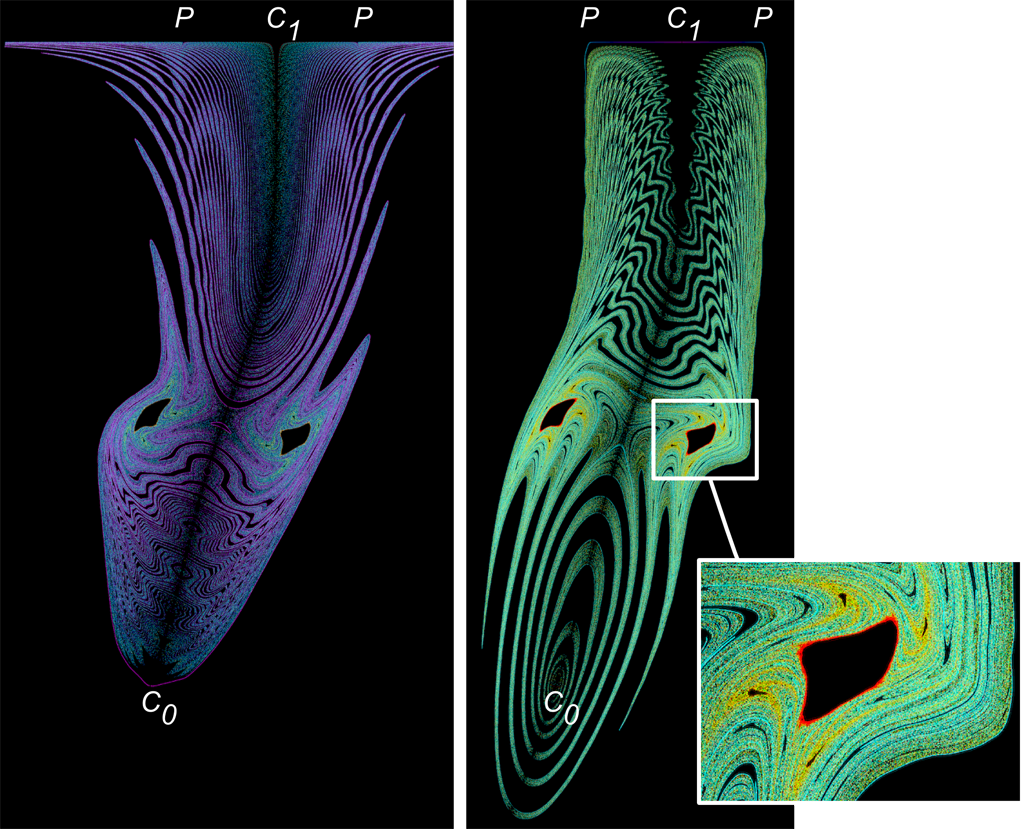
A pattern often found in regions of recirculating flow is the vortex ring. Smoke rings and vortex breakdown bubbles are two familiar instances of this pattern. A vortex ring requires at least two critical points, and in fact this minimum number is observed in many synthetic or real-world examples. Based on this observation, we propose a visualization technique utilizing a Poincaré section that contains the pair of critical points. The Poincaré section by itself can be taken as a visualization of the vortex ring, especially if streamlines are seeded on the stable and unstable manifolds of the critical points. The resulting image reveals the extent of the structure, and more interestingly, regions of chaos and islands of stability. As a next step, we describe for the case of incompressible flow an algorithm for finding invariant tori in an island of stability. The basic idea is to find invariant closed curves in the Poincaré plane, which are then taken as seed curves for stream surfaces. For visualization the two extremes of the set of nested tori are computed. This is on the inner side the periodic orbit toward which the tori converge, and on the outer side, a torus which marks the boundary between ordered and chaotic flow, a distinction which is of importance for the mixing properties of the flow. For the purpose of testing, we developed a simple analytical model of a perturbed vortex ring based on Hill's spherical vortex. Finally, we applied the proposed visualization methods to this synthetic vector field and to two hydromechanical simulation results.
|
Available Files
[BibTeX]
[DOI]
[PDF]
|
|


