Efficient Visualization of Lagrangian Coherent Structures by Filtered AMR Ridge Extraction
IEEE Transactions on Visualization and Computer Graphics, vol. 13, no. 6, pp. 1456–1463, 2007.

|

|
|
|
||||||
|
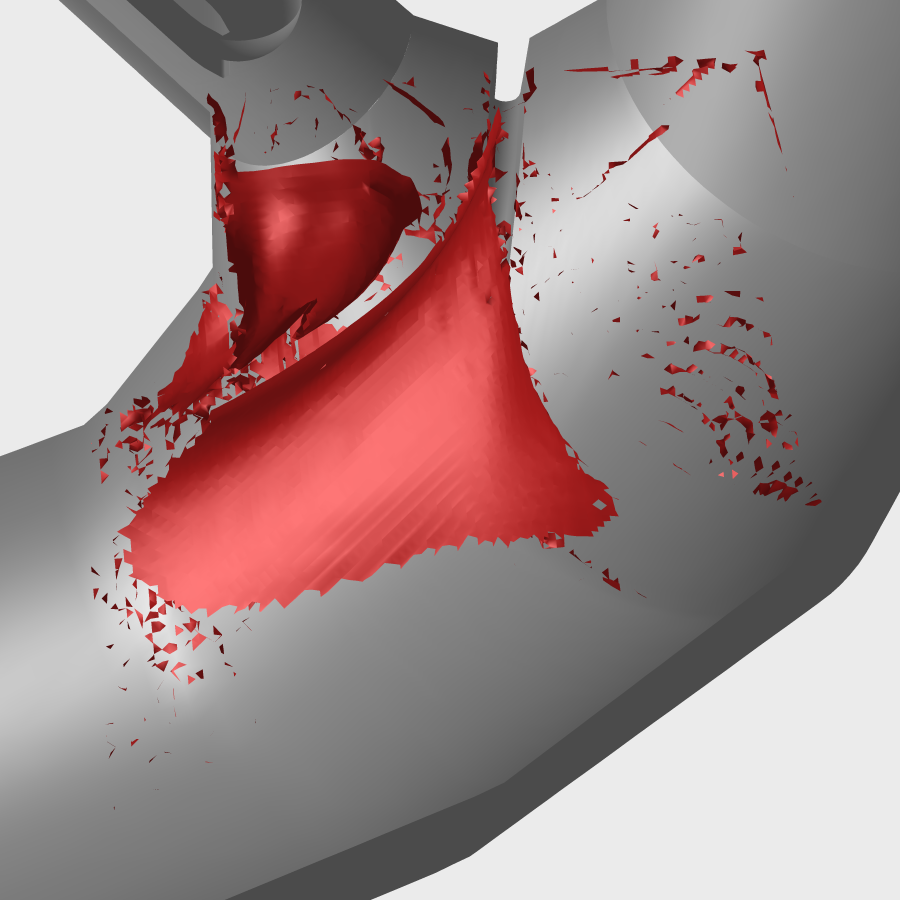
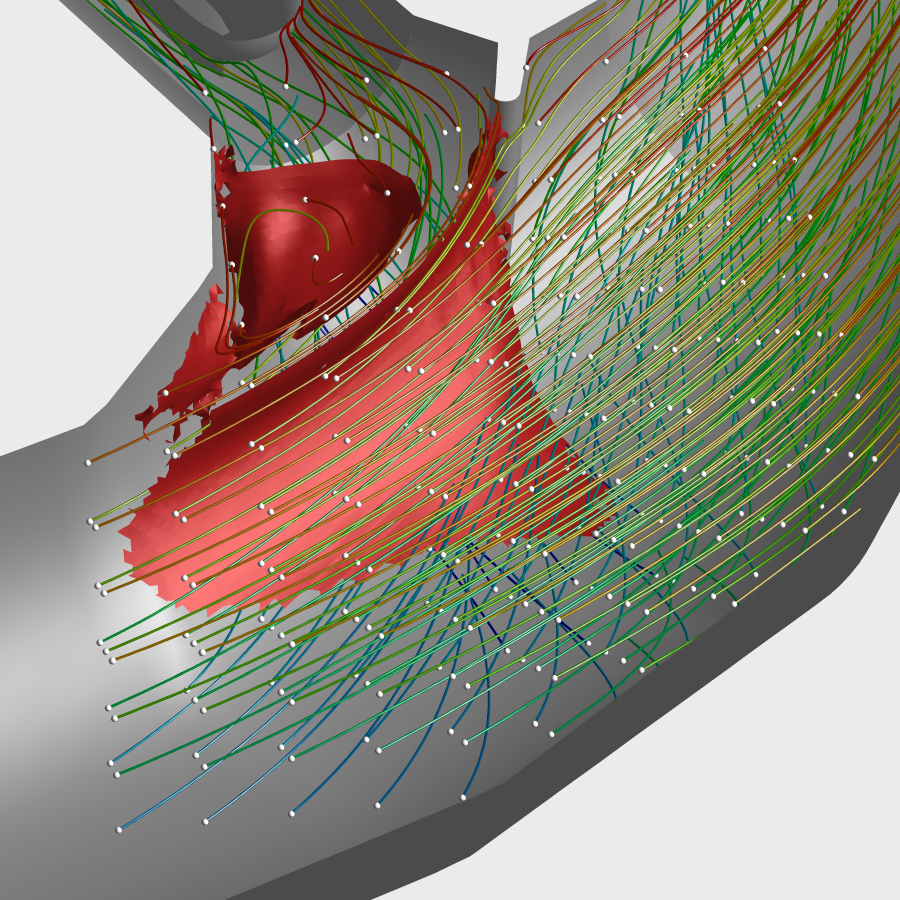
AbstractThis paper presents a method for filtered ridge extraction based on adaptive mesh refinement. It is applicable in situations where the underlying scalar field can be refined during ridge extraction. This requirement is met by the concept of Lagrangian coherent structures which is based on trajectories started at arbitrary sampling grids that are independent of the underlying vector field. The Lagrangian coherent structures are extracted as ridges in finite Lyapunov exponent fields computed from these grids of trajectories. The method is applied to several variants of finite Lyapunov exponents, one of which is newly introduced. High computation time due to the high number of required trajectories is a main drawback when computing Lyapunov exponents of 3-dimensional vector fields. The presented method allows a substantial speed-up by avoiding the seeding of trajectories in regions where no ridges are present or do not satisfy the prescribed filter criteria such as a minimum finite Lyapunov exponent. |
|||||||||
Available Files[BibTeX] [DOI] [PDF] [Video] [Video] [Video] [Slides] |
|||||||||
