Time-Dependent Visualization of Lagrangian Coherent Structures by Grid Advection
In Topological Methods in Data Analysis and Visualization, Springer Berlin Heidelberg, pp. 151–165, 2011.
|
|

|
|||||||
|
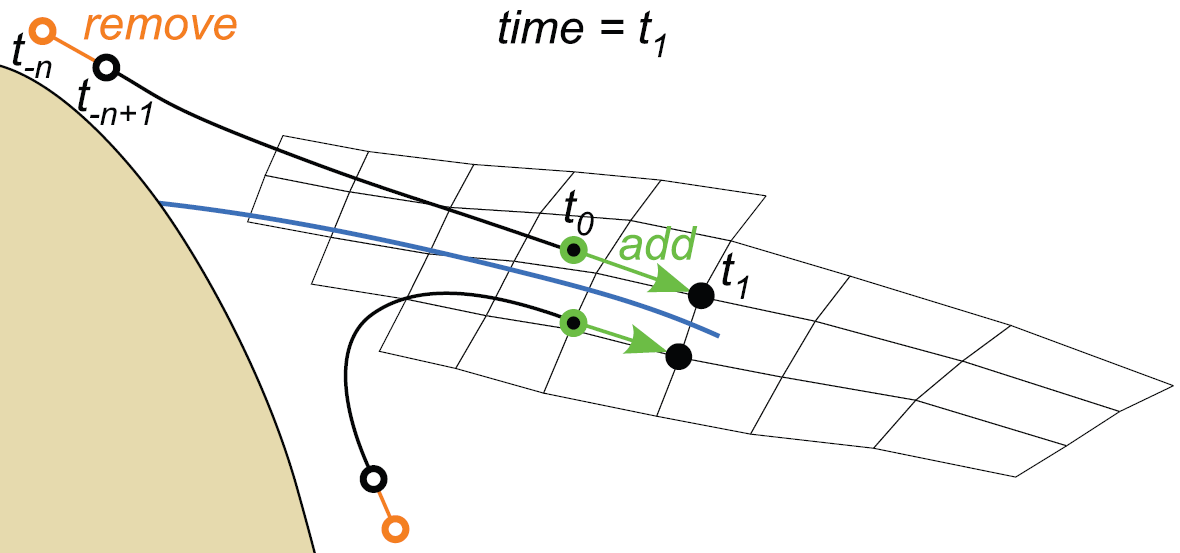
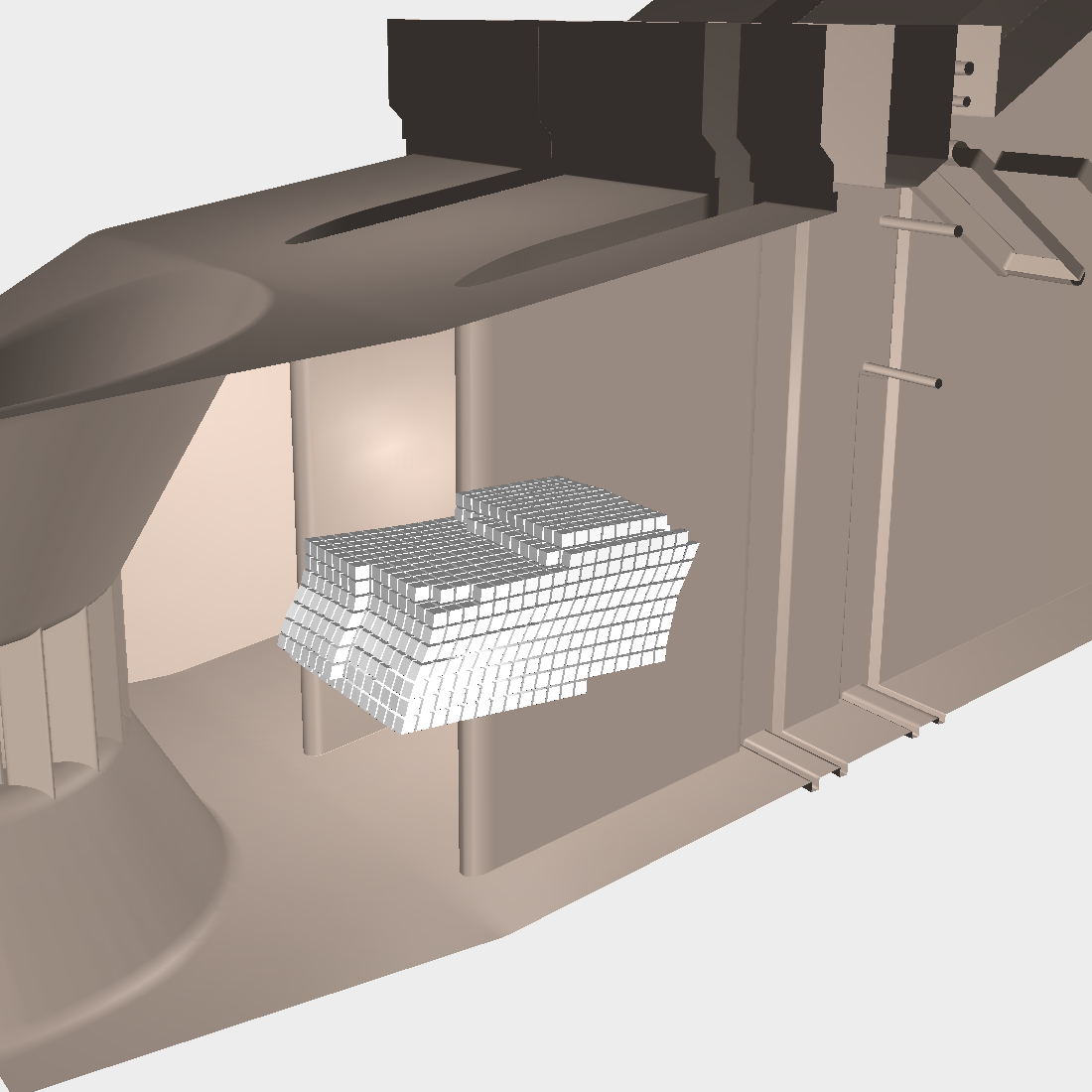
AbstractLagrangian coherent structures play an important role in the analysis of unsteady vector fields because they represent the time-dependent analog to vector field topology. Nowadays, they are often obtained as ridges in the finite-time Lyapunov exponent of the vector field. However, one drawback of this quantity is its very high computational cost because a trajectory needs to be computed for every sample in the space-time domain. A focus of this paper are Lagrangian coherent structures that are related to predefined regions such as boundaries, i.e. related to flow attachment and flow separation phenomena. It presents an efficient method for computing the finite-time Lyapunov exponent and its height ridges only in these regions, and in particular,grid advection for the efficient computation of time series of the finite-time Lyapunov exponent, exploiting temporal coherence. |
|||||||||
Available Files[BibTeX] [DOI] [PDF] [Slides] |
|||||||||
