M. Üffinger,
F. Sadlo,
M. Kirby,
C. Hansen,
T. Ertl:
In Short Paper Proceedings of Eurographics 2012,
pp. 61–64,
2012.
|

|
|
Abstract
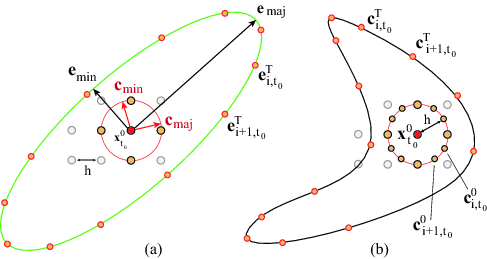
We present a framework for different approaches to finite-time Lyapunov exponent (FTLE) computation for 2D vector fields, based on the advection of seeding circles. On the one hand it unifies the popular flow map approach with techniques based on the evaluation of distinguished trajectories, such as renormalization. On the other hand it allows for the exploration of their order of approximation (first-order approximation representing the flow map gradient). Using this framework, we derive a measure for nonlinearity of the flow map, that brings us to the definition of a new FTLE approach. We also show how the nonlinearity measure can be used as a criterion for flow map refinement for more accurate FTLE computation, and we demonstrate that ridge extraction in supersampled FTLE leads to superior ridge quality.
|
Available Files
[BibTeX]
[DOI]
[PDF]
|
|


