G. M. Machado,
F. Sadlo,
T. Ertl:
In Proceedings of International Workshop on Vision, Modeling and Visualization (VMV),
pp. 17–24,
2013.

|
|

|
|
Abstract
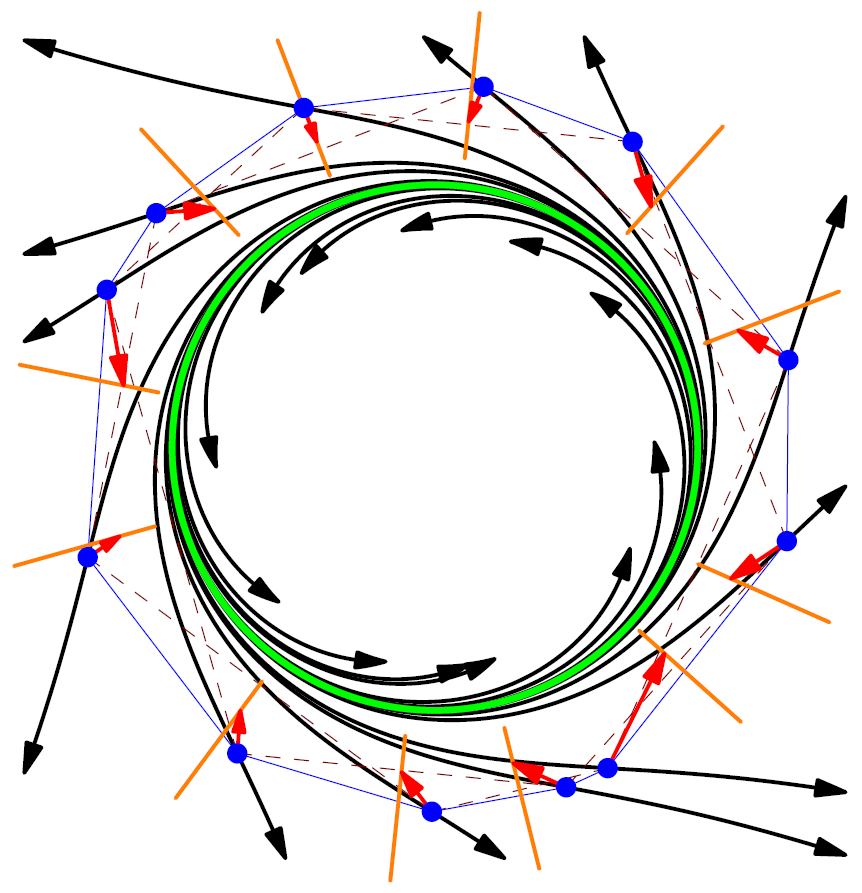
We present local extraction of bifurcation lines together with extraction of their manifolds, a topological feature that has not yet been sufficiently recognized in scientific visualization. The bifurcation lines are extracted by a modification of the vortex core line extraction techniques due to Sujudi-Haimes, and Roth-Peikert, both formulated using the parallel vectors operator. While the former provides acceptable results only in configurations with high hyperbolicity and low curvature of the bifurcation lines, the latter operates only well in configurations with low hyperbolicity but is able to perform well with strong curvature of the bifurcation lines, however, with the drawback that it often fails to provide a solution. We present refinement of the solutions of the parallel vectors operator as a means to improve both criteria and, in particular, to refine the solutions of the Sujudi-Haimes criterion in cases where the Roth-Peikert criterion fails. We exemplify our technique on synthetic data, data from computational fluid dynamics, and on magnetohydrodynamics data. As a particularly interesting application, we demonstrate that our technique is able to extract saddle-type periodic orbits locally, and in case of high hyperbolicity at higher accuracy than traditional techniques based on integral curves.
|
Available Files
[BibTeX]
[DOI]
[PDF]
|
|



