L. Hofmann,
F. Sadlo:
Computer Graphics Forum,
vol. 40,
no. 3,
pp. 111–122,
2021.
|
|
Abstract
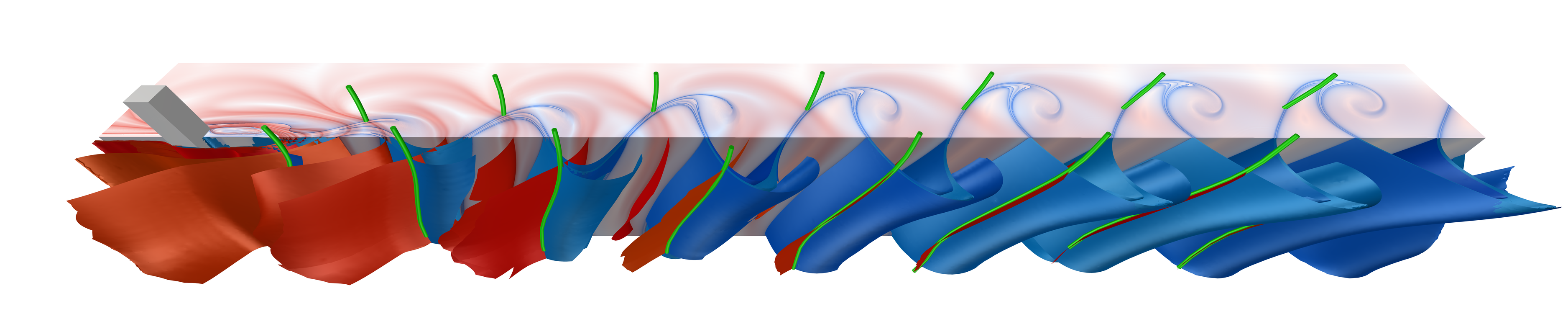
We present an approach to local extraction of 3D time-dependent vector field topology. In this concept, Lagrangian coherent structures, which represent the separating manifolds in time-dependent transport, correspond to generalized streak manifolds seeded along hyperbolic path surfaces (HPSs). Instead of expensive and numerically challenging direct computation of the HPSs by intersection of ridges in the forward and backward finite-time Lyapunov exponent (FTLE) fields, our approach employs local extraction of respective candidates in the four-dimensional space-time domain. These candidates are subsequently refined toward the hyperbolic path surfaces, which provides unsteady equivalents of saddle-type critical points, periodic orbits, and bifurcation lines from steady, traditional vector field topology. In contrast to FTLE-based methods, we obtain an explicit geometric representation of the topological skeleton of the flow, which for steady flows coincides with the hyperbolic invariant manifolds of vector field topology. We evaluate our approach on analytical flows, as well as data from computational fluid dynamics, using the FTLE as a ground truth superset, i.e., we also show that FTLE ridges exhibit several types of false positives.
|
Available Files
[BibTeX]
[DOI]
[PDF]
[Highres PDF]
[Technical Addendum]
[Video]
[Video]
[Talk]
[Slides]
|
|

